Une grande portion des statistiques théoriques implique des suppositions qui s’appliquent rarement aux données réelles et la plupart des données réelles comportent des complexités multiples, de sorte que certaines combinaisons n’ont parfois pas été étudiées en détail auparavant. Par exemple, il existe une littérature substantielle portant sur le traitement des données manquantes, la façon dont on doit ajuster pour des autocorrélations temporelles (séries temporelles) ou des structures de données hiérarchiques (modèles multi-niveaux), et le traitement des variables comportant trop de zéros. Toutefois, je doute fort qu’une seule étude méthodologique n’ait examiné comment gérer ces quatre problématiques simultanément ou considéré comment elles peuvent interagir entre elles. Par conséquent, les littératures théoriques et méthodologiques en statistiques sont généralement incapables de fournir des réponses claires à des milliers de combinaisons et défis semblables, auxquels nous sommes confrontés chaque jour. L’approche décrite ici constitue donc en grande partie une réponse à la nécessité de traiter les données complexes lorsque qu’il n’existe pas de conseils clairs pour de tels cas spécifiques.
Le test d’hypothèse comporte un sens scientifique et un sens statistique, que nous rejetons conjointement dans la plupart des circonstances. D’un point de vue scientifique, un devis de recherche avec un test d’hypothèse est trop « blanc ou noir » et nous empêche souvent de réaliser quand les données nous disent que nous posions la mauvaise question. D’un point de vue statistique, le test d’hypothèse découle en partie d’une incapacité historique à calculer facilement des valeurs précises de p, ce qui n’est plus le cas avec les ordinateurs. Le principe des statistiques est d’estimer l’incertitude dans un monde probabiliste; tenter de prendre cette incertitude et de la réduire en « vrai » ou « faux » sur la seule foi d’un seuil arbitraire de valeur de p est à l’antithèse des principes de base de la probabilité.
Bon nombre d’ouvrages statistiques utilisent des règles arbitraires et des arbres de décision (ex. utilisation de statistiques non-paramétriques pour un n < 30). Il y a généralement de bonnes raisons d’appliquer de telles règles dans la majorité des cas, mais il existe aussi de nombreuses exceptions (ex. certains tests non-paramétriques peuvent engendrer une perte de puissance non justifiée pour un n < 30 lorsque les connaissances préalables nous indiquent que la distribution est normale, et les tests non-paramétriques imposent également des suppositions sur la distribution n’étant pas nécessairement justifiées). Le fait d’appliquer ces règles aveuglément nous garantit de mauvaises prises de décision dans une minorité de situations, à tout le moins non négligeable. La seule solution acceptable est de comprendre d’où viennent les règles et de faire preuve de discernement au cas par cas.
Bien souvent, les variables que l’on souhaite étudier ne peuvent pas être mesurées directement, ce qui nous force à combiner plusieurs méthodes afin de générer des variables représentant au mieux le vrai processus biologique (ou sociologique, etc.) à l’étude. Par exemple, si nous voulons étudier la morphologie des bébés à la naissance en ajustant pour le fait que certains sont nés prématurément, il importerait avant tout de faire une analyse en composantes principales incluant plusieurs mesures morphologiques pour en extraire les aspects clés. Les axes générés par cette analyse seraient ensuite soumis à une régression par spline cubique sur l’âge gestationnel à la naissance, et les résidus de cette régression nous donneraient la variable désirée. Bien que complexe, de telles approches sont souvent essentielles si nous souhaitons mesurer le vrai processus d’intérêt au lieu d’une mesure approximative directe.
Il s’agit sans doute du point le plus critique. Exécuter une analyse statistique implique des milliers de choix arbitraires qui ont tous le potentiel de changer les résultats. Faut-il exclure une mesure de taille de 203 cm en tant que donnée aberrante? Quelle variable devrions-nous utiliser pour estimer le statut socio-économique? Sur quelles variables devrions-nous utiliser une transformation log? Quel type de procédure d’estimation du maximum de vraisemblance serait de rigueur? La nécessité de faire de si nombreux choix remet sérieusement en question les résultats d’une seule analyse, quelle qu’elle soit. Si vous n’en croyez rien, essayez l’outil ici pour voir comment un nombre restreint de tels choix peut complètement changer les résultats d’une analyse visant à déterminer si l’économie américaine se porte mieux sous les Républicains ou les Démocrates. Il n’existe qu’une seule solution à ce problème: effectuer beaucoup, beaucoup de versions différentes de l’analyse afin de vérifier que les résultats sont stables et dans la négative, quels choix affectent les résultats. Nous effectuons typiquement des dizaines de milliers d’analyses pour une seule publication. Si les résultats concordent, nous pouvons commencer à être plus confiants à l’égard des conclusions; s’ils ne concordent pas, nous devons comprendre pourquoi ils diffèrent avant de pouvoir publier.
Notre approche telle que décrite précédemment, fondée sur la répétition des analyses, génère tellement de résultats qu’il est souvent difficile de les examiner manuellement. Nous effectuons donc des analyses portant sur les effets de nos approches analytiques alternatives sur les résultats. Par exemple, si nous avons cinq facteurs que nous pouvons modifier pour une analyse de régression avec respectivement 3, 4, 2, 2, et 10 options, nous pouvons effectuer 3x4x2x2x10=480 analyses afin de couvrir toutes les combinaisons possibles. Nous pouvons ensuite inclure les 480 coefficients de régression obtenus dans une méta-régression, dans laquelle nous analysons les effets sur les résultats de chacune des options pour chacun des facteurs. De telles approches ne sont pas toujours nécessaires mais constituent un moyen rigoureux d’évaluer la stabilité des résultats et les facteurs pouvant les influencer.
Particulièrement pour les variables continues, l’un des aspects les plus fondamentaux – et pourtant l’un des plus délicats – des statistiques est de considérer la distribution. La variable est-elle distribuée normalement? Est-ce que ce qui semble être une distribution normale cache en fait une densité mélangée due à une covariable importante? Que nous dit notre compréhension de la biologie sur les distributions des variables, comment les transformer, comment traiter les données aberrantes, etc.? Le discours sur les distributions en statistiques appliquées est simple: il faut tenter d’obtenir une variable normalement distribuée (avec une transformation log, par exemple). Le discours sur les distributions en statistiques théoriques est précis: explorer les différences subtiles entre les distributions théoriques qui peuvent ne pas être distinguables empiriquement dans la plupart des jeux de données. Aucune de ces approches n’est suffisante dans la plupart des cas. Il est rarement possible d’investir trop de temps à réfléchir aux distributions des variables, à ce qu’elles nous disent sur la biologie et comment les traiter dans les analyses subséquentes.
En lien avec le point précédent, l’une des erreurs majeures dans plusieurs articles scientifiques est de traiter la variable mesurée comme le phénomène d’intérêt. Dans la plupart des cas, ce n’est pas justifié : ce que nous pouvons mesurer n’est qu’une faible approximation du vrai processus (biologique, sociologique, etc.). Considérez la figure ci-dessous, qui représente quatre façons différentes selon lesquelles le seuil clinique pour le diagnostic du diabète (126 mg/dl) peut illustrer un vrai processus sous-jacent. La majorité des personnes supposent, parce que nous disons qu’une personne a le diabète si son taux de sucre sanguin est supérieur à 126 mg/dl, que le graphique du coin supérieur gauche est le bon. Toutefois, lorsque confrontés à ces quatre graphiques, nous serions tous d’accord pour dire que les modèles du coin supérieur droit et du coin inférieur gauche sont plus près de la réalité. Même si l’on continue à mesurer le diabète comme une variable dichotome, le fait d’avoir considéré le processus sous-jacent peut nous amener à exécuter différents modèles statistiques et poser différentes questions scientifiques. (En fait, différents modèles statistiques posent TOUJOURS des questions scientifiques différentes…) L’absence de prise en considération des processus sous-jacents mène les chercheurs à ignorer l’erreur de mesure dans le meilleur des cas et, plus généralement, à poser des questions absurdes ou générer des résultats erronés.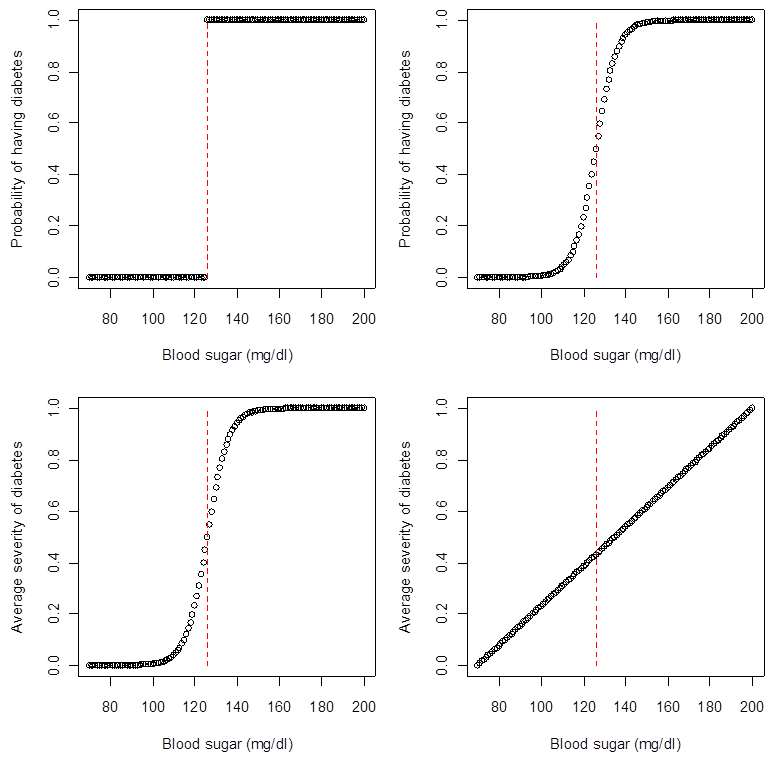
Notre cerveau est conçu pour simplifier les choses et l’un des moyens les plus efficaces d’y parvenir est de remarquer l’incertitude temporairement pour ensuite l’ignorer. Nous lisons un article scientifique, prenons note des limites de l’étude reconnues par les auteurs, mais lorsque nous citons l’article ou en appliquons les principes, nous assumons simplement qu’il est vrai (ou faux). Nous procédons de la même façon en analyse statistique, ignorant l’incertitude issue des analyses précédentes et mettons ainsi beaucoup trop de foi dans l’analyse finale (et l’estimation finale de l’incertitude). Il n’y a pas de recette miracle pour éviter cette incertitude; il importe seulement d’être conscient du risque et de tenter de faire les ajustements appropriés.
Les approches décrites précédemment – particulièrement la répétition des résultats dans plusieurs analyses et contextes – ne constituent pas une panacée. Notamment, plusieurs analyses risquent de contenir le même biais. S’il importe de contrôler pour le statut socio-économique (SSE) dans une analyse et que les mesures de SSE sont trop imprécises, différentes analyses risquent de montrer le même effet erroné parce qu’elles ont en commun le même biais.
Nous avons tous des biais personnels et des résultats que nous attendons ou espérons observer. Dans certains cas, il peut s’agir de biais professionnels ou financiers, tels que la nécessité de publier dans un journal à haut facteur d’impact en vue d’une promotion ou une compagnie pharmaceutique tentant d’obtenir une approbation réglementaire. Plusieurs des règles entourant la pratique statistique sont conçues pour éviter ce genre de biais – quelques exemples incluent la formulation d’une hypothèse a priori et l’ajustement pour des tests multiples. Toutefois, ces règles sont loin d’être suffisantes, comme le démontre la probabilité beaucoup plus élevée qu’une étude supporte un produit pharmaceutique si celle-ci est financée par une compagnie avec des intérêts financiers. Ces règles ne sont peut-être pas inutiles, mais les biais constituent toujours un problème majeur et les règles ont un coût substantiel : elles nous rendent rigides et incapables de suivre une évidence peu importe où elle nous mène. Par exemple, un médicament destiné à réduire la mortalité due au cancer du sein pourrait ne pas accomplir ses effets désirés, mais par ailleurs améliorer substantiellement la qualité de vie. Nous ne devrions pas rejeter la conclusion qui concerne la qualité de vie simplement parce nous ne l’avions pas prédite, mais devrions être prudents quant à une surinterprétation si l’effet est faible ou marginal.
La meilleure façon de résoudre le problème de biais mentionné ci-dessus ne réside pas en une série de règles, mais plutôt en une tentative honnête de la part des chercheurs de combattre ces biais et de se prouver qu’ils ont tort. Évidemment, tous les chercheurs ne feront pas preuve de la même efficacité et certains n’essaieront même pas. Il revient donc aux réviseurs et aux éditeurs d’exiger une approche plus critique et plus nuancée envers la recherche dans les articles que nous révisons.
Générer des milliers de résultats par article constitue un défi d’écriture, si l’on souhaite un article clair et concis. Notre approche est la suivante : (1) Exécuter un nombre suffisant d’analyses pour lesquelles nous sommes confiants quant au message clé à retenir (même si le message est nuancé ou subtile). (2) Écrire l’article autour de ce message clé. (3) Inclure suffisamment de détails dans la section Méthodes et Information supplémentaire pour montrer au lecteur que nous avons essayé maintes et maintes variantes de l’analyse. (4) Pour plus de simplicité, omettre la description des analyses qui ne sont pas primordiales à la compréhension du message clé, même si elles nous ont aidés à nous y rendre. (5) Écrire des articles en un sens qui encouragera les autres chercheurs à utiliser cette approche.
